Matematika SMP: Barisan dan Deret Aritmatika
Matematika SMP: Barisan dan Deret Aritmatika - Barisan dan deret aritmatika merupakan materi penting yang dipelajari oleh siswa SMP Kelas VIII dengan Kurikulum 2013. Barisan aritmatika merupakan barisan bilangan-bilangan dengan syarat nilai setiap sukunya didapatkan dari suku sebelumnya melalui penjumlahan atau pengurangan dengan suatu bilangan. Selisih atau beda antara nilai suku-suku yang berdekatan selalu sama yaitu b. Nilai suku pertama dilambangkan dengan a.
Untuk mengetahui nilai suku ke-n dari suatu barisan arimatika kita dapat menggunakan rumus sebagai berikut:
dimana: Un = suku ke-n, a adalah suku pertama dan b adalah selisih antara suku-suku yang berdekatan.
Sedangkan deret aritmatika merupakan penjumlahan suku-suku dari sebuah barisan aritmatika. Jumlah n-suku suatu barisan aritmatika dapat ditemukan dengan menggunakan rumus sebagai berikut:
atau
Contoh Soal dan Penyelesaian Barisan dan Deret Aritmatika
Contoh 1:
Suku ke-40 dari barisan 7, 5, 3, 1, … adalah …
Pembahasan:
Diketahui: a = 7
b = –2
ditanya
Jawab:
= 7 + 39 . (-2)
= 7 + (-78)
= – 71
Jadi, suku ke-40 barisan aritmatika tersebut adalah –71.
Contoh 2:
Rumus suku ke-n dari barisan 5, –2, –9, –16, … adalah …
Pembahasan:
Diketahui: a = 5
b = –7
Ditanya: rumus suku ke-n barisan aritmatika tersebut = ?
Jawab:
Jadi, rumus suku ke-n barisan aritmatika tersebut adalah
Contoh 3:
Dalam suatu gedung pertunjukkan disusun kursi dengan baris paling depan terdiri dari 12 kursi, baris kedua berisi 14 kursi, baris ketiga berisi 16 kursi, dan seterusnya. Banyaknya kursi pada baris ke-20 adalah …
Pembahasan:
Diketahui: a = 12
b = 2
Ditanyakan
Jawab:
Jadi, banyaknya kursi pada baris ke-20 adalah 50 kursi.
Contoh 4:
Rumus jumlah n suku pertama deret bilangan 2 + 4 + 6 + … +
Pembahasan:
Diketahui: a = 2, b = 2
Ditanya: rumus jumlah n suku pertama barisan aritmatika tersebut = ?
Jawab:
Jadi, rumus jumlah n suku pertama barisan aritmatika tersebut adalah
Contoh 5:
Diketahui deret aritmatika dengan suku ke-3 adalah 24 dan suku ke-6 adalah 36. Jumlah 15 suku pertama deret tersebut adalah …
Pembahasan:
Diketahui
Ditanya:
Jawab:
Sebelum kita mencari nilai dari  , kita akan mencari nilai a dan b terlebih dahulu dengan cara eliminasi dan subtitusi dari persamaan
, kita akan mencari nilai a dan b terlebih dahulu dengan cara eliminasi dan subtitusi dari persamaan  dan
dan  .
.
Sebelumnya mari ingat lagi bahwa 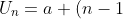b) sehingga
sehingga  dan
dan  dapat ditulis menjadi
dapat ditulis menjadi 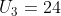
Eliminasi a menggunakan persamaan i dan ii.
a + 2b = 24
a + 5b = 36 –
-3b = -12
b = 4
Lalu, substitusikan nilai b = 4 ke salah satu persamaan (contoh persamaan i).
a + 2b = 24
a + 2 . 4 = 24
a + 8 = 24
a= 24 – 8
a = 16
Setelah mendapatkan nilai a dan b, baru kita bisa mencari nilai dari
Jadi, jumlah 15 suku pertama deret tersebut adalah 660.
Contoh 6:
Diketahui barisan aritmetika mempunyai suku ke-2 bernilai 4 dan suku ke-8 bernilai 22. Tentukanlah suku ke-15 dari barisan tersebut !
Penyelesaian:
$U_n = a + (n - 1)b$
$U_2 = 4 → a + b = 4$ . . . . (1)
$U_8 = 22 → a + 7b = 22$ . . . . (2)
Eliminasi persamaan (1) dan (2)
$a + b = 4$
$a + 7b = 22$
-------------------------- $-$
$6b = 18$
$b = 3$
$a = 1$
$U_{15}= a + 14b$
$U_{15}= 1 + 14\times 3$
$U_{15}= 43$
.
Contoh 7:
Diketahui suku ke-3 dan suku ke-15 barisan aritmetika berturut-turut adalah 4 dan 40. Hitunglah Jumlah 20 suku pertama barisan aritmetika tersebut.
Penyelesaian:
$U_n = a + (n - 1)b$
$U_3 = 4 → a + 2b = 4$ . . . . (*)
$U_{15} = 40 → a + 14b = 40$ . . . . (**)
Eliminasi persamaan (*) dan (**)
$a + 2b = 4$
$a + 14b = 40$
----------------------- $-$
$12b = 36$
$b = 3$
$a = -2$
$S_n = \dfrac n2(2a + (n - 1)b)$
$S_{20}= \dfrac{20}{2}(2.(-2) + 19.3)$
$= 10.(-4 + 57)$
$= 10.53$
$= 530$
Contoh 8:
Diketahui suku ke-3 dan ke-7 suatu barisan aritmetika berturut-turut adalah 28 dan 44. Tentukanlah jumlah 25 suku pertama dari barisan aritmetika tersebut !
Penyelesaian :
$U_n = a + (n - 1)b$
$U_3 = 28 → a + 2b = 28$ . . . . (1)
$U_7 = 44 → a + 6b = 44$ . . . . (2)
Eliminasi persamaan (1) dan (2)
$a + 2b = 28$
$a + 6b = 44$
---------------------- $-$
$4b = 16$
$b = 4$
$a = 20$
$S_{n}=\frac{n}{2}(2a+(n-1)b)$
$S_{25}=\frac{25}{2}(2\times 20+24\times 4)$
$= \dfrac{25}{2}(40 + 96)$
$= \dfrac{25}{2}.136$
$= 1.700$
Contoh 9:
Suku ke-6 dan ke-10 suatu deret aritmetika berturut-turut adalah 20 dan 32. Hitunglah jumlah 10 suku pertama deret aritmetika tersebut.
Penyelesaian:
$U_6 = 20 → a + 5b = 20$ . . . . (1)
$U_{10} = 32 → a + 9b = 32$ . . . . (2)
Eliminasi persamaan (1) dan (2)
$a + 5b = 20$
$a + 9b = 32$
----------------------- $-$
$4b = 12$
$b = 3$
$a = 5$
$S_n = \dfrac {n}{2}(2a + (n - 1)b)$
$S_{10}= \dfrac{10}{2}(2.5 + 9.3)$
$= 5.(10 + 27)$
$= 5.37$
$= 185$
Contoh 10.
Rudi berinvestasi dengan menabung uangnya. Setiap bulan besar tabungan bertambah secara tetap dimulai dari bulan pertama Rp50.000,00, bulan kedua Rp55.000,00, bulan ketiga Rp60.000,00, dan seterusnya.Hitunglah jumlah tabungan Rudi selama 10 bulan.
Penyelesaian.
$a = 50000$
$b = 5000$
$n = 10$
$S_n = \frac {n}{2}(2a + (n - 1)b)$
$S_{10}= \frac{10}{2}(2x50.000 + 9x5.000)$
$= 5x(100.000 + 45.000)$
$= 5x145.000$
$= Rp725.000,00$
Setelah membaca tentang barisan dan deret aritmetika, sub materi tentang barisan dan deret yang mesti dibaca adalah tentang barisan dan deret geometri di postingan berikutnya.
Semoga bermanfaat.
Posting Komentar untuk "Matematika SMP: Barisan dan Deret Aritmatika"
Pembaca boleh bebas berkomentar selama isi komentar berhubungan dengan isi postingan, menggunakan kalimat yang santun dan berguna bagi pengembangan blog ini.