Matematika SMP Kelas VII: Bilangan Pecahan
Pengantar Pecahan
Bilangan Pecahan telah diajarkan sejak tingkat sekolah dasar. Hampir semua materi pecahan di SMP telah diajarkan di SD namun, yang membedakannya adalah peningkatan kesulitn materi akibat perbedaan pola pikir anak-anak terkait dengan pembelajaran matematika sekolah. Tentu saja di smp kelas VII, materi pecahan diajarkan dengan mulai sedikit demi sedikit meninggalkan model konkrit.
Konsep ini menyatakan pecahan sebagai hasil bagi suatu bilangan dengan bilangan yang lain. Konsep semacam ini dapat diilustrasikan dengan di bawah ini.
Untuk menentukan 3 ÷ 4, maka kita bagi 3 dengan 2 terlebih dahulu. Dari sini kita akan mendapatkan satu setengah. Setelah itu, kita bagi dua satu setengah tersebut untuk mendapatkan ¾.
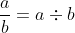
(3) Pecahan sebagai konsep perbandingan.
Berdasarkan gambar di atas, kita dapat melihat bahwa
Membandingkan pecahan juga dapat dilakukan dengan mengubah pecahan-pecahan tersebut menjadi pecahan senilai yang berpenyebut sama. Karena KPK dari 4 dan 7 adalah 28, maka
Setelah itu, kita bandingkan pembilang kedua pecahan tersebut. Karena 21 > 20 maka
Secara umum, membandingkan dua pecahan dapat dilakukan dengan cara berikut.
Tonton video tentang membandingkan pecahan berikut:
Untuk menyamakan penyebut dua pecahan, kita juga dapat mengalikan penyebut kedua pecahan tersebut. Hasil kali kedua penyebut tersebut tidak selalu KPK dari kedua penyebut tersebut. Setelah dua pecahan tersebut memiliki penyebut yang sama, kita tinggal menjumlahkan kedua pecahan tersebut.
Pengurangan Pecahan. Pengurangan pecahan dapat dilakukan seperti dalam penjumlahan pecahan. Pertama, jika perlu, samakan penyebut pecahan-pecahan yang diberikan, kemudian kurangi pembilang-pembilang pecahan dan biarkan penyebutnya tetap.
Video Operasi Penjumlahan dan Pengurangan Pecahan:
Untuk mengalikan kedua pecahan tersebut, pertama kita gambar pecahan 4⁄5. Selanjutnya kita arsir 2⁄3 dari daerah 4⁄5. Perhatikan Gambar berikut
Dari ilustrasi tersebut kita dapat melihat bahwa hasil kalinya dapat diperoleh dengan mengalikan pembilang kedua pecahan, per hasil kali dari penyebut.
Untuk sembarang dua pecahan
Pembagian Pecahan. Pembagian pecahan dapat dimaknai serupa dengan pembagian bilangan cacah. Salah satu makna dalam pembagian bilangan cacah dapat direpresentasikan dengan pengurangan berulang. Hal ini akan kita gunakan untuk memaknai pembagian pecahan.
Perhatikan contoh berikut.
Pembelajaran matematika SMP Kelas VII semester 1 materi pecahan ditekankan untuk membantu siswa mencapai standar kompetensi yaitu memahami sifat-sifat operasi hitung bilangan dan penggunaanya dalam pemecahan masalah. Kompetensi dasarnya adalah melakukan operasi hitung bilangan pecahan; dan siswa diharapkan dapat menggunakan sifat-sifat hitung bilangan pecahandalam pemecahan masalah.
Materi pecahan yang diajarkan di SMP kelas VII antara lain: Pengertian Bilangan Pecahan, Pengertian dan Cara Menentukan Pecahan Senilai, Menyederhanakan Bilangan Pecahan, Menyatakan Hubungan Antara Dua Pecahan, Menentukan Letak Pecahan Pada Garis Bilangan, Menentukan Pecahan yang Nilainya di Antara Dua Pecahan, Pecahan sebagai Perbandingan Bagian dari Keseluruhan, Mengubah Pecahan Biasa Menjadi Pecahan Campuran, Mengubah Bentuk Pecahan ke Bentuk Desimal, Mengubah Bentuk Pecahan ke Bentuk Persen, Mengubah Bentuk Pecahan ke Bentuk Permil, Penjumlahan dan Pengurangan Pecahan, Sifat-sifat pada penjumlahan dan pengurangan pecahan, Operasi Perkalian Pecahan, Sifat-sifat dan Invers perkalian pada pecahan dan Operasi Pembagian Pecahan.
Pecahan (dalam bahasa inggris fraction, berasal dari kata Latin fractio yang berarti memecah. Oleh karena itu, istilah bilangan pecah juga sering juga disebut pecahan. Istilah pecahan dapat digunakan untuk merujuk suatu bilangan yang ditulis dalam bentuk
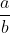 dimana b ≠ 0. Perlu diperhatikan penggunaan simbol tersebut sebagai bilangan atau angka.
dimana b ≠ 0. Perlu diperhatikan penggunaan simbol tersebut sebagai bilangan atau angka.
Misalnya, jika kita menyatakan bahwa bilangan yang terletak di atas disebut pembilang dan bilangan yang di bawah disebut penyebut, maka pecahan yang kita maksud di situ adalah suatu simbol atau angka. Akan tetapi jika kita mengatakan, “Jumlahkan 13 dan 12 ,” maka yang kita maksud adalah pecahan sebagai suatu bilangan.
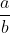 , bilangan b menunjukkan banyaknya bagian yang sama dalam keseluruhan, sedangkan bilangan yang di atas, a, menunjukkan banyaknya bagian yang diperhatikan. Gambar berikut ini menggambarkan pecahan 3⁄8.
, bilangan b menunjukkan banyaknya bagian yang sama dalam keseluruhan, sedangkan bilangan yang di atas, a, menunjukkan banyaknya bagian yang diperhatikan. Gambar berikut ini menggambarkan pecahan 3⁄8.
Pengertian dan Konsepsi dari Pecahan
Pecahan (dalam bahasa inggris fraction, berasal dari kata Latin fractio yang berarti memecah. Oleh karena itu, istilah bilangan pecah juga sering juga disebut pecahan. Istilah pecahan dapat digunakan untuk merujuk suatu bilangan yang ditulis dalam bentuk
Misalnya, jika kita menyatakan bahwa bilangan yang terletak di atas disebut pembilang dan bilangan yang di bawah disebut penyebut, maka pecahan yang kita maksud di situ adalah suatu simbol atau angka. Akan tetapi jika kita mengatakan, “Jumlahkan 13 dan 12 ,” maka yang kita maksud adalah pecahan sebagai suatu bilangan.
Pada topik pecahan di SMP, pembilang dan penyebut suatu pecahan adalah bilangan bulat. Bilangan yang seperti ini juga disebut dengan bilangan rasional. Akan tetapi, secara umum, pembilang dan pecahan suatu pecahan adalah sembarang bilangan real asalkan penyebutnya tidak sama dengan nol.
Pecahan dapat dijelaskan dengan menggunakan tiga konsep, yaitu konsep
Pecahan dapat dijelaskan dengan menggunakan tiga konsep, yaitu konsep
(1) Pecahan sebagai sebagian dari keseluruhan.
Pecahan dinyatakan sebagai konsep sebagian dari keseluruhan artinya pecahan digunakan untuk menytakan hubungan antara bagian-bagian dari sesuatu yang utuh.
Pada pecahan
(2) Pecahan sebagai konsep pembagian
Konsep ini menyatakan pecahan sebagai hasil bagi suatu bilangan dengan bilangan yang lain. Konsep semacam ini dapat diilustrasikan dengan di bawah ini.

|
Untuk sembarang bilangan a dan b, dengan b ≠0 |
Pecahan juga dapat digunakan sebagai perbandingan. Misalkan banyaknya siswa laki-laki adalah sepertiga dari banyaknya siswa perempuan.
Pecahan-Pecahan Senilai
Pecahan Senilai dan Cara Menentukan Pecahan Senilai- Pecahan yang berbeda dapat bernilai sama asalkan perbandingannya tetap. Pecahan tersebut dinamakan pecahan senilai. Pecahan senilai merupakan materi yang diajarkan pada siswa kelas 4 sekolah dasar dimana pada Kompetensi Dasar 3.1
Menentukan Pecahan Senilai dengan Membagi atau Mengalikan Pembilang dan Penyebut dengan Bilangan yang Sama. Kompetensi ini sangat penting dimiliki siswa kelas 4 karena akan sangat berguna sebagai materi prasyarat pada materi pecahan selanjutnya maupun materi materi matematika yang lain.
Tonton juga video : Pecahan Senilai dan Cara Menentukan Pecahan Senilai berikut ini:
Tonton juga video : Pecahan Senilai dan Cara Menentukan Pecahan Senilai berikut ini:
Untuk memahami tentang pecahan senilai, tiga kegiatan yang dapat dilakukan adalah menggunakan garis bilangan, menggunakan gambar yang diarsir dan mengalikan pembilang dan penyebut dari pecahan dengan sebuah bilangan yang sama.
Pecahan senilai merujuk pada pecahan yang nilainya tetap sama ketika pembilang dan penyebut dari sebuah pecahan dikalikan atau dibagi dengan bilangan yang sama. Perlu diingat bahwa bilangan yang dikalikan bukanlah 0 sebab 0/0 =tak terhingga.
1. Menentukan Pecahan Senilai dengan Garis Bilangan
Cara pertama untuk menentukan pecahan senilai adalah dengan menggunakan Garis Bilangan. Garis bilangan merupakan alat atau model yang bermanfaat bagi pembelajaran pecahan senilai setelah model konkrit dan model gambar.
Perhatikan garis bilangan berikut.
Jika nilai pecahan pada garis bilangan di atas berada pada garis putus-putus yang sama, maka pecahan tersebut senilai. Misalnya, sebagai berikut.
2. Menentukan Pecahan Senilai dengan Menggunakan Gambar
Perhatikan gambar berikut.
Daerah persegi panjang pada gambar di atas dibagi menjadi beberapa bagian yang sama. Bilangan di bawah masing-masing gambar menunjukkan luas daerah yang diarsir.
Karena luas daerah yang diarsir pada masing-masing gambar tersebut sama, maka pecahan
bernilai sama, dan disebut pecahan-pecahan senilai.
3. Menentukan Pecahan Senilai dengan Membagi atau Mengalikan Pembilang dan Penyebut dengan Bilangan yang Sama
Untuk mengetahui hubungan pecahan-pecahan yang senilai, perhatikan uraian berikut.
Berdasarkan contoh di atas dapat dikatakan bahwa pecahan yang senilai dapat diperoleh, jika pembilang dan penyebut dari suatu pecahan dikalikan dengan bilangan yang sama.
Selanjutnya, perhatikan hubungan pecahan-pecahan berikut.
Berdasarkan contoh di atas dapat dikatakan bahwa pecahan yang senilai dapat diperoleh dengan membagi pembilang dan penyebut suatu pecahan dengan bilangan yang sama.
Berdasarkan uraian di atas dapat disimpulkan bahwa untuk menentukan pecahan senilai dapat dilakukan dengan mengalikan pembilang dan penyebut dengan bilangan yang sama atau dilakukan dengan membagi pembilang dan penyebut dengan bilangan yang sama.
Menyamakan Penyebut
Adakalanya kita diberikan dua pecahan dengan penyebut yang berbeda. Misalkan 1⁄4 dan 1⁄6. Gambar berikut menunjukkan bahwa banyaknya bagian-bagian dari kedua pecahan tersebut berbeda.
Jika masing-masing 1⁄6 bagian kita bagi menjadi dua bagian yang sama dan masing-masing 1⁄4 bagian kita bagi menjadi tiga bagian yang sama, maka masing-masing akan memiliki 12 bagian yang sama. Sehingga diperoleh dua pecahan yang senilai dengan dua pecahan sebelumnya, yaitu 3⁄12 dan 2⁄12, tetapi penyebutnya sama.
Tonton Video : Pecahan Sederhana dan Cara Menyederhanakan Pecahan
Tonton Video : Pecahan Sederhana dan Cara Menyederhanakan Pecahan
Membandingkan Pecahan
Untuk membandingkan dua pecahan, kita dapat menggunakan Gambar di bawah ini.Berdasarkan gambar di atas, kita dapat melihat bahwa
Setelah itu, kita bandingkan pembilang kedua pecahan tersebut. Karena 21 > 20 maka
| Untuk sembarang pecahan dimana b dan d positif,  jika dan hanya jika ad < bc dan  jika dan hanya jika ad > bc |
Tonton video tentang membandingkan pecahan berikut:
Operasi Penjumlahan dan Pengurangan Pecahan
Penjumlahan Pecahan. Penjumlahan dua pecahan dapat diilustrasikan dengan menggabungkan dua nilai. Perhatikan contoh berikut.Antok belajar matematika selama ½ jam, dan dilanjutkan belajar fisika 1⁄3 jam. Berapa jamkah Antok belajar matematika dan fisika?Salah satu cara untuk menyelesaikan masalah ini adalah dengan menggunakan gambar. Gambar berikut ini menunjukkan pecahan ½ dan 1⁄3.
Baca Juga:
Operasi Penjumlahan, Operasi Pengurangan, Operasi Perkalian dan Operasi Pembagian Pecahan
Untuk memudahkan dalam penjumlahan pecahan, kita samakan penyebut dua pecahan yang diberikan. KPK dari 2 dan 3 adalah 6, maka
Selanjutnya kita ilustrasikan penjumlahan 3⁄6 dan 2⁄6 pada Gambar berikut.
Dari gambar tersebut kita dapat menuliskan
Sehingga, untuk menjumlahkan dua pecahan, pertama kita pastikan penyebut kedua pecahan tersebut sama. Setelah itu kita jumlahkan pecahan tersebut dengan menjumlahkan pembilang-pembilangnya, dan membiarkan penyebut tetap.
Untuk sembarang dua pecahan
Perhatikan contoh berikut.
Bintang diberi ¾ kg buah apel oleh tantenya. Karena dia memiliki adik, maka dia memberikan 1⁄6 kg apel tersebut kepada adiknya. Berapa kg sisa apel yang dimiliki oleh Bintang?
Untuk menentukan sisa apel yang dimiliki Bintang, kita cari hasil
Pengurangan kedua pecahan tersebut dapat diilustrasikan oleh Gambar berikut.
Berdasarkan gambar tersebut kita dapat melihat bahwa
Jadi, sisa apel yang dimiliki Bintang adalah 7⁄12 kg
| Untuk sembarang dua pecahan |
Video Operasi Penjumlahan dan Pengurangan Pecahan:
Operasi Perkalian dan Pembagian Pecahan
Perkalian Pecahan. Perkalian pecahan akan lebih mudah jika diilustrasikan dengan menggunakan luas daerah. Misalkan kita akan menghitungUntuk mengalikan kedua pecahan tersebut, pertama kita gambar pecahan 4⁄5. Selanjutnya kita arsir 2⁄3 dari daerah 4⁄5. Perhatikan Gambar berikut
Dari ilustrasi tersebut kita dapat melihat bahwa hasil kalinya dapat diperoleh dengan mengalikan pembilang kedua pecahan, per hasil kali dari penyebut.
Untuk sembarang dua pecahan
Pembagian Pecahan. Pembagian pecahan dapat dimaknai serupa dengan pembagian bilangan cacah. Salah satu makna dalam pembagian bilangan cacah dapat direpresentasikan dengan pengurangan berulang. Hal ini akan kita gunakan untuk memaknai pembagian pecahan.
Dari Gambar di atas tampak bahwa kita dapat mengurangi ¾ dengan 1⁄8 sebanyak 6 kali. Sehingga,
Kemudian bagaimana jika nanti hasil baginya bukan berupa bilangan cacah. Dengan kata lain, bagaimana jika nanti setelah dikurangi secara berulang akan menghasilkan sisa? Untuk kasus ini, perhatikan ilustrasi yang ditunjukkan Gambar berikut.
Gambar di atas mengilustrasikan .
Ketika 5/6 dikurangi oleh 1/3 sebanyak 2 kali, maka akhirnya dihasilkan sisa. Jika kita bandingkan sisanya dengan pembaginya, maka kita dapat melihat bahwa sisa tersebut sama dengan setengahnya
pembagi. Sehingga,
Selain dengan menggunakan gambar, pembagian pecahan juga dapat dilakukan dengan mengubah pembagian menjadi perkalian dengan membalik pembaginya.pembagi. Sehingga,
Perhatikan contoh berikut.
Sehingga, ide dalam pembagian tersebut adalah membuat pembaginya menjadi 1. Dengan cara yang serupa kita dapat membagi pecahan seperti berikut.
| Untuk sembarang pecahan |
Sumber: Beberapa bagian dari postingan ini diambil dari Modul Pecahan. Yosep Dwi Kristanto, M.Pd. Universitas Sanata Dharma Yogyakarta
Untuk memahami materi pecahan di SMP, para siswa perlu mempelajari kembali pecahan yang telah diajarkan di Sekolah dasar. Berikut ini merupakan tautan untuk mempelajari kembali materi pecahan SD agar siswa lebih mantap dan mudah belajar pecahan di SMP.
Untuk memahami materi pecahan di SMP, para siswa perlu mempelajari kembali pecahan yang telah diajarkan di Sekolah dasar. Berikut ini merupakan tautan untuk mempelajari kembali materi pecahan SD agar siswa lebih mantap dan mudah belajar pecahan di SMP.
- Garis Besar Materi Pecahan di Kelas IV Sekolah Dasar
- Merubah Beberapa Bilangan Desimal Tidak Sejenis menjadi Bilangan Desimal Sejenis untuk Operasi Penjumlahan dan Pengurangan Bilangan Desimal
- Pecahan Senilai dan Cara Menentukan Pecahan Senilai
- Pembelajaran Penjumlahan dan Pengurangan Desimal di Kelas 5 Sekolah Dasar
- Soal dan Jawaban Ujian Nasional Matematika Sekolah Dasar Pokok Bahasaan Pecahan
Semoga postingan ini bermanfaat. Materi pecahan SMP akan diposting di blog ini secara berkala.





































Posting Komentar untuk "Matematika SMP Kelas VII: Bilangan Pecahan"
Pembaca boleh bebas berkomentar selama isi komentar berhubungan dengan isi postingan, menggunakan kalimat yang santun dan berguna bagi pengembangan blog ini.